10655. Virus tree 2
You are given a
tree with n vertices and n – 1 edges. The vertices are numbered from
1 to n, and the i-th edge connects vertices ai and bi.
You have k colors available. For each vertex in
the tree, you choose one of the k
colors to paint it, subject to the following condition:
·
If the distance between two different vertices x and y is less than or equal to two, then x and y have different
colors.
How many ways are
there to color the tree? Find the answer modulo 109 + 7.
Input. The first line contains two
numbers n and k (1 ≤ n, k ≤ 105). Each of the following
n – 1 lines contains two integers ai and bi (1 ≤ ai, bi ≤ n).
Output. Print the number of ways to
color the tree modulo 109 + 7.
|
Sample input 1 |
Sample output 1 |
|
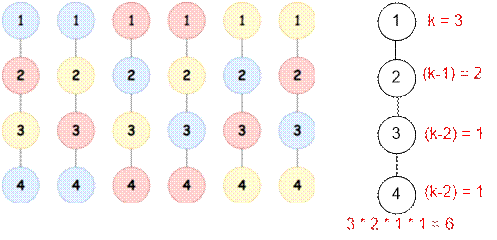
4 3 1 2 2 3 3 4 |
6 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
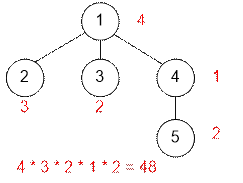
5 4 1 2 1 3 1 4 4 5 |
48 |
SOLUTION
graphs – depth first search
Algorithm analysis
Let’s start coloring the tree
from vertex 1. It can be colored with k
colors.
Suppose we are at vertex v. If it has no parent (v = 1), then its children can be colored
with k – 1 colors. If v has a parent, then its children can be
colored with k – 2 colors. Since the
distance between the children of vertex v
is 2, they cannot be colored with the same color.
If vertex v has a parent, then the first child of v can be colored with k –
2 colors, the second child with k – 3
colors, and so on.
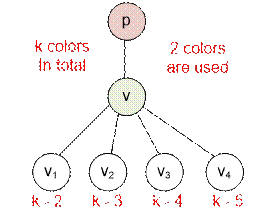
It remains to multiply the
numbers of colors that can be used to color each vertex.
Example
For the first example, there are 6 ways of
coloring:
Let’s consider the second test. Next to
each vertex, we’ll indicate the number of colors it can be colored with. For
example, vertex 5 can be colored with 2 colors, as its color must not match the
colors of vertices 1 and 4. The total number of ways to color the tree is equal
to 4 * 3 * 2 * 1 * 2 = 48.
Algorithm implementation
Store the input graph in the
adjacency list g. Declare a constant MOD
for the modulo.
#define MOD
1000000007
vector<vector<int>>
g;
The dfs
function returns the number of ways to color the tree rooted at vertex v modulo MOD = 109 + 7. The parent
of vertex v is p. Vertex v can be colored with col
colors.
int dfs(int v, int col, int p =
-1)
{
long long res
= col;
We
are at vertex v. In the variable cnt,
we keep track of the number of colors that cannot be used to paint the children
of vertex v. Initially, set cnt = 1, since the children of vertex v cannot have the same color as vertex v. If vertex v has a parent (p ≠
-1), then the children of vertex v also
cannot have the color of v’s parent.
int cnt
= 1;
if (p
>= 0) cnt++;
Iterate
over the sons to of the vertex v.
for (int to : g[v])
if (to != p)
{
The
vertex to can be colored with k – cnt
colors. With each son, the cnt value
will be increased by 1.
res = (res * dfs(to, k - cnt, v)) % MOD;
cnt++;
}
return res;
}
The
main part of the program. Read the input data.
scanf("%d %d",
&n, &k);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d
%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Start
the depth-first search from vertex 1. Vertex number 1 can be colored with k colors.
res = dfs(1, k);
Print
the answer.
printf("%lld\n",
res);
Python implementation
Set the maximum depth of the Python interpreter stack to the
specified limit.
import
sys
sys.setrecursionlimit(1000000)
Declare
a constant MOD for the modulo.
MOD
= 1000000007
The dfs
function returns the number of ways to color the tree rooted at vertex v modulo MOD = 109 + 7. The parent
of vertex v is p. Vertex v can be colored with col
colors.
def dfs(v, col, p = -1):
res = col
We
are at vertex v. In the variable cnt,
we keep track of the number of colors that cannot be used to paint the children
of vertex v. Initially, set cnt = 1, since the children of vertex v cannot have the same color as vertex v. If vertex v has a parent (p ≠
-1), then the children of vertex v also
cannot have the color of v’s parent.
cnt = 1
if p >= 0:
cnt += 1
Iterate
over the sons to of the vertex v.
for to in g[v]:
if to != p:
The
vertex to can be colored with k – cnt
colors. With each son, the cnt value
will be increased by 1.
res = (res * dfs(to, k - cnt, v)) % MOD
cnt += 1
return res
The
main part of the program. Read the input data.
n, k
= map(int, input().split())
g =
[[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Start
the depth-first search from vertex 1. Vertex number 1 can be colored with k colors.
res
= dfs(1, k)
Print
the answer.
print(res)